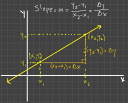
Everything's Relative `(frac (Deltay) (Deltax))`
An Introduction to Functions
Sep-22-2021 | Views: 1145 | (0)
A function describes a relationship between two or more variables. Consider the equation `y=x+1`. This equation describes a relationship between the variable `y` and the variable `x`, and it tells you that the value of `y` is always `1` more than the value of `x`.
The syntax `f(x)` tells you that `f` is a function, and it takes `x` as an input. `f(x)` defines a relationship between two things that are represented mathematically by variables, `x` and `y`, where `y=f(x)`. I have seen many students confused by the function notation, `f(x)`. I think it's just a result of not having much experience with functions, or maybe having a previous teacher who wasn't good at explaining what they are, or both.
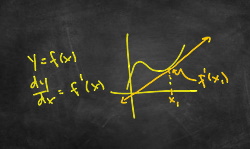 Anyway, when you see `f(x)` it is pronounced, "`f` of `x`". The `f` and the `x` are not separate; it's not `f` times `x` as some students want to think. They are one thing that defines a relationship between a variable `x` and a variable `y`. Where is `y`, you say? `y` comes from evaluating the function, `f(x)`, at specific values of `x`; `y` is the output of the function. So `y` is `f(x)`. Sometimes you will see just the `f` without the `(x)` part. Don't think that's something different; it's not. The `f` by itself refers to the function in general; the set of operations that are performed on the input to the function, whatever that input happens to be. `f(x)` refers to an instance of the function, `f`. A function has to have an input, and the input is whatever is inside the parentheses. Let's go through a couple of examples and hopefully, this will make more sense.
Anyway, when you see `f(x)` it is pronounced, "`f` of `x`". The `f` and the `x` are not separate; it's not `f` times `x` as some students want to think. They are one thing that defines a relationship between a variable `x` and a variable `y`. Where is `y`, you say? `y` comes from evaluating the function, `f(x)`, at specific values of `x`; `y` is the output of the function. So `y` is `f(x)`. Sometimes you will see just the `f` without the `(x)` part. Don't think that's something different; it's not. The `f` by itself refers to the function in general; the set of operations that are performed on the input to the function, whatever that input happens to be. `f(x)` refers to an instance of the function, `f`. A function has to have an input, and the input is whatever is inside the parentheses. Let's go through a couple of examples and hopefully, this will make more sense.
Suppose you have a function, `f(x)=x^2 + 2x + 1`. This takes `x` as its input (what's inside the parentheses) and the ... (More)
What is Slope? What does it tell you?
Aug-17-2021 | Views: 1365 | (13)
What is slope?
Slope is one of the most versatile and applicable concepts in mathematics. In its simplest form, it's just two numbers and a division operation, a fraction, and yet it's the basis for all of Calculus!
What does it tell you?
If you have two variables that are related such that the value of the one is dependent on the value of the other, then the slope of their relationship tells you how much the value of the dependent variable (typically `y`) will change if the value of the independent variable (typically `x`) changes. It defines a measure of the relationship between these two variables. In mathematics it is standard practice to use the letter `m` to represent slope so when you see `m`, think slope.
How is it calculated?
The slope of a linear functionA linear function has ... (More)
Introduction
Aug-01-2021 | Views: 844 | (0)

Everything's Relative will be my home for all my math articles covering concepts that I think are important for students to understand as they are learning mathematics. I'm calling it this because it's something that I firmly believe is true in all things in life, plus it refers to a mathematical concept, slope, which I think is one of the most important and versatile concepts in mathematics. I will get into it in depth in my first post which will be all about slope.
Here, I will cover topics over a variety of math subjects from middle-school-level to college-level courses. My intent is to help you understand mathematics; why certain things work, and why they don't. Additionally, I'll present it in a mathematically correct way. There are too many mathematics blog sites already on the web that are just not very good in terms of how the material is presented. Some are just incorrect in places; others are correct but not written very well. There are a lot of high school math teachers that have mathematics ... (More)
Popular Tags
Popular Tags
here are the poupluar tags...